Strides and padding

Padding

So, we were looking into residual block, and have been building on it back to the basics of convolution and now we are at padding. The reason being convolution layers in Deep Learning frameworks are coupled with padding and strides operations to the layers.
Without the arguments passed, the strides is 1, padding is 0. Simply put, the kernel slides by 1 across the feature map and there are no zeros added around the feature map. Let's implement padding operation on a matrix, then implement it with a convolution operation. The below code adds a single line of zeros around the input.

a = torch.tensor([
    [1, 2, 3],
    [4, 5, 6]
])

def naive_padding(feature_map, zeros_around=0):
    shape = feature_map.shape
    mod_shape = (torch.tensor(shape) + (zeros_around * 2)).tolist()
    out_map = torch.zeros(mod_shape)
    out_map[zeros_around: -zeros_around, zeros_around: -zeros_around] = feature_map
    return out_map

print(naive_padding(a, 1))

            tensor([
    [0., 0., 0., 0., 0.],
    [0., 1., 2., 3., 0.],
    [0., 4., 5., 6., 0.],
    [0., 0., 0., 0., 0.]
])
          

Implementing the same with PyTorch, we have

import torch.nn.functional as F
def torch_padding(feature_map, zeros_around=0):
    p1d = (
        zeros_around, zeros_around,
        zeros_around, zeros_around
    )
    return F.pad(a, p1d, "constant", 0)
print(torch_padding(a, 1))
# ensuring the outputs are identical
assert torch.equal(naive_padding(a, 1), torch_padding(a, 1))

            tensor([
[0, 0, 0, 0, 0],
[0, 1, 2, 3, 0],
[0, 4, 5, 6, 0],
[0, 0, 0, 0, 0]])
          

Now, let's do a convolution and zero padding together in our code for the above matrix and using the sharpen kernel from the previous section. This is easy since we have both functions implemented, let's just call the padding function then pass the result to the convolution function.

def naive_convolution(feature_map, kernel):
    (H, W) = feature_map.shape
    SIZE = kernel.shape[0]
    out_H, out_W = H-SIZE+1, W-SIZE+1
    output_naive = torch.zeros(out_H, out_W)
    for i in range(out_H):
        for j in range(out_W):
            patch = feature_map[i:i+SIZE, j:j+SIZE]
            value = torch.sum(patch*kernel)
            output_naive[i, j] = value
    return output_naive

# sharpen kernel
kernel = torch.ones(3, 3) * -1
kernel[::2, ::2] = 0
kernel[1, 1] = 5

out = naive_convolution(
    naive_padding(a, 1), kernel
)
print(out)

            tensor([[-1.,  1.,  7.],
        [14., 13., 22.]])
          

Let's now introduce the official neural network implementation of convolution for 2d inputs, that is, the feature map and filter, the use of the term filter since the the input has abstract dimensions, to get the result above.
Because PyTorch's Conv2d has randomized weights to be optimized and not statically defined, let's sort of hack our way by setting the weights to our sharpen kernel, but never will you do this cause this weights are to be updated by the optimizer, which, if you were keen in our section on perceptron, is just the part that updated the weights of the perceptron iteratively, take it as you may a simple optimizer.

import torch.nn as nn
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=1)

def override_kernel_weights(module, kernel):
    with torch.no_grad():
        conv.weight[:] = kernel
        conv.bias[:] = 0
    return conv

conv = override_kernel_weights(conv, kernel)
print(conv.state_dict().keys())
print(list(conv.parameters()))

            odict_keys(['weight', 'bias'])
[Parameter containing:
tensor([[[[-1.,  0., -1.],
        [ 0.,  5.,  0.],
        [-1.,  0., -1.]]]], requires_grad=True), Parameter containing:
tensor([-0.2403], requires_grad=True)]
          

Trainable neural network modules always have weights and biases irrespective of how the layer is architected.
From the code above, we see parameters to the Conv2d, first, in_channels, which is just the depth of input, 1 for the input we will use below, 3 for RGB image, etc
The next parameter, out_channels, is so the stack of filters will be such that the output after the convolution returns a single channel. If you set this to 3, filter will have depthwise stack of 3 kernels, each with randomized weights and their own biases, which when convolved with input single channel, gives an output of 3 channels.
kernel_size is very well self explanatory and padding is us wanting a single line of zeros around the input feature map.
We don't need the bias so we'll set it to zero.

res = conv(a.view(1,1,*a.shape).to(torch.float))
print(res)

            tensor([[[[-1.,  1.,  7.],
        [14., 13., 22.]]]], grad_fn=<ConvolutionBackward0>)
          

Don't you just love every piece of the puzzle fitting so perfectly.This is exactly the same result we got from the naive convolution just above.

Strided convolutions

We know from layman terms that a stride is the step the kernel takes to move to the next patch in the input feature map, technically known as the distance between spatial locations where the convolution kernel is applied. Previously, we have been dealing with strides of 1, but now, let's take it a step further, no pun intended, and implement changing strides for convolution operation. The formula given a convolution considering padding and striding is as shown below

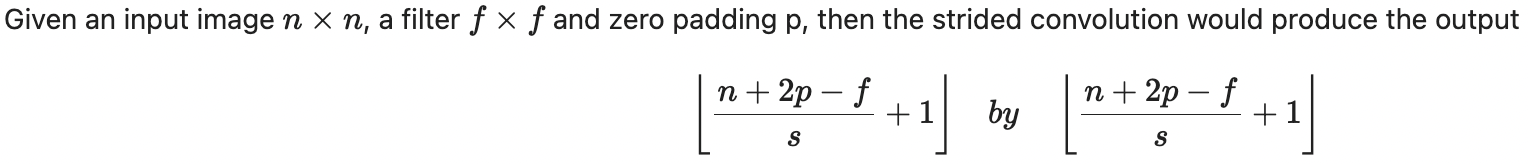
Working with the input matrix and the kernel below, let's now implement the strided convolution

def naive_strided_convolution(feature_map, kernel, strides=1):
    (H, W) = feature_map.shape
    SIZE = kernel.shape[0]
    # the line below is as seen from the formula, 
    # with p done before this so it is implicitly taken
    # into consideration (note the 2 * zeros_around)
    # in the naive_padding implementation
    out_H = out_W = int(((H-SIZE)/strides)+1)
    output_naive = torch.zeros(out_H, out_W)
    for i in range(out_H):
        for j in range(out_W):
            r = i * strides
            c = j * strides
            patch = feature_map[r:r+SIZE, c:c+SIZE]
            value = torch.sum(patch*kernel)
            output_naive[i, j] = value
    return output_naive

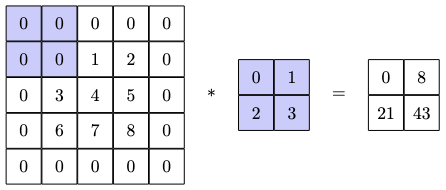
Now using the implemented strided convolution to get the result for the defined input and the kernel

in_ = torch.arange(9).reshape(3,3)
kernel = torch.arange(4).reshape(2,2)
out = naive_strided_convolution(
    naive_padding(in_, 1), kernel, strides=2
)
print(out)

            tensor([[ 0.,  8.],
        [21., 43.]])
          

Going back to PyTorch's defined definition of convolution with the striding and padding used in the previous codebase, the programmatic implementation becomes

import torch.nn as nn
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=2, padding=1, stride=2)
def override_kernel_weights(module, kernel):
    with torch.no_grad():
        conv.weight[:] = kernel
        conv.bias[:] = 0
    return conv
conv = override_kernel_weights(conv, kernel)
res = conv(in_.view(1,1,*in_.shape).to(torch.float))
print(res)

            tensor([[[[ 0.,  8.],
        [21., 43.]]]], grad_fn=<ConvolutionBackward0>)
          